Универсальные учебные действия на уроках математики в 1 классе
26.10.2015 Елена Сергеева 0 Comments
Тип материала: Методическая разработка
ФИО автора: Пономарёва Валентина Николаевна
Место работы: Ширяевская СОШ Иловлинского муниципального района
Должность автора: Учитель начальных классов
*Материалы публикуются в авторской редакции
Универсальные учебные действия на уроках математики в 1 классе
Приоритетной целью школьного образования становится общекультурное, личностное и познавательное развитие учащихся, обеспечивающие такую ключевую компетенцию образования, как «научить учиться» (Слайд 2). Учащийся сам должен стать «архитектором и строителем» образовательного процесса.
Достижение данной цели становится возможным благодаря формированию системы универсальных учебных действий (УУД).
Когда-то очень давно Герберт Спенсер сказал: «Великая цель образования – это не знания, а действия».
Универсальные учебные действия можно сгруппировать в четыре основных блока (Слайд 3): 1) личностные;
2) познавательные;
3) регулятивные;
4) коммуникативные.
Мой опыт работы в начальной школе показывает, что моделирование уроков по формированию УУД – дело непростое, но сегодня – это требование времени.
Овладение ими происходит в контексте разных учебных предметов. Каждый предмет раскрывает свои собственные, специфические возможности для формирования УУД, определяемые, в первую очередь, функцией учебного предмета и его предметным содержанием.
Я работаю по УМК «Начальная школа 21 века» и хочу рассказать о возможности формирования УУД учащихся на уроках математики в 1 классе.
Познавательные универсальные учебные действия
Предмет «Математика» направлен прежде всего на развитие познавательных универсальных учебных действий.
Для успешного обучения в начальной школе должны быть сформированы следующие познавательные универсальные учебные действия (Слайд 4): общеучебные, логические, действия постановки и решения проблем.
Общеучебные универсальные действия (Слайд 5):
— самостоятельное выделение и формулирование познавательной цели;
— поиск и выделение необходимой информации;
— структурирование знаний;
— осознанное и произвольное построение речевого высказывания;
— выбор наиболее эффективных способов решения задач;
Особую группу общеучебных универсальных действий составляют знаково-символические действия: моделирование – преобразование объекта из чувственной формы в модель; преобразование модели с целью выявления общих законов. Возрастные психологические особенности младших школьников делают необходимым формирование моделирования как универсального учебного действия, для математики это действие представляется наиболее важным, так как создаёт важнейший инструментарий для развития у детей познавательных универсальных действий. Поэтому задания учебника первого класса знакомят учащихся с общепринятыми в математике моделями (Слайд 6.).
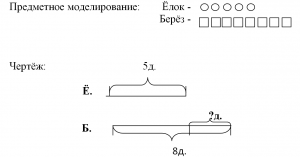
Например, решая задачу: «Около школы посадили 5 ёлок, а берёз 8.На сколько посадили берёз больше, чем ёлок?», после анализа текста задачи можно составить несколько моделей (по выбору).
Логические универсальные действия:
— синтез – составление целого из частей;
— выбор оснований и критериев для сравнения, классификации объектов;
— установление причинно-следственных связей;
— построение логической цепи рассуждений;
— доказательство;
— выдвижение гипотез и их обоснование.
Отличительной чертой учебника математики УМК «Начальная школа XXl века» является широкое использование продуктивных заданий, требующих целенаправленного использования и, как следствие, развития таких важнейших мыслительных операций, как анализ, синтез, классификация, сравнение, аналогия. (Все задания учебника, сопровождающиеся инструкциями «Сравни», «Разбей на группы», «Найди истинное высказывание» и т.д.)
Приведу несколько примеров:
1) Анализ объектов с целью выделения признаков:
1, 3, 5, 7, 9.
Что объединяет числа? (однозначные; каждое следующее число увеличивается на 2);
2)Построение логической цепи рассуждений: найти правило построения числового ряда.
3 6 9 12 ?
Постановка и решение проблемы:
— Формулирование проблемы;
— Самостоятельное создание способов решения проблем творческого и поискового характера.
Личностные универсальные действия:
Личностные действия позволяют сделать учение осмысленным, обеспечивают ученику значимость решения учебных задач, увязывания их с реальными жизненными целями и ситуациями. Они направлены на осознание, исследование и принятие жизненных ценностей и смыслов; позволяют сориентироваться в нравственных нормах, правилах, оценках вырабатывать свою жизненную позицию в отношении мира, окружающих людей, самого себя и своего будущего.
Применительно к учебной деятельности следует выделить три вида личностных действий (Слайд 7):
1) Личностное, профессиональное, жизненное самоопределение ;
2) Смыслообразование :
— развития познавательных интересов, учебных мотивов;
— формирования мотивов достижения и социального признания;
— мотива, реализующего потребность в социально значимой и социально
оцениваемой деятельности.
3) Нравственно-этическая ориентация – направлена на уважение истории и культуры всех народов, развитие толерантности; знание основных моральных норм (справедливое распределение, взаимопомощь, правдивость, честность, ответственность); развитие доброжелательности, доверия и внимательности к людям, готовности к сотрудничеству и дружбе, оказанию помощи тем, кто в ней нуждается; формирование установки на здоровый и безопасный образ жизни; формирование чувства прекрасного и эстетических чувств на основе знакомства с мировой и отечественной художественной культурой. Здесь используются знания учащимися культуры нашего народа, достопримечательности и исторические памятники нашего села, природа села. Часто использую небольшие сообщения о нашем хуторе.
Все без исключения задания учебника ориентированы на достижение личностных результатов, так как они предлагают не только найти решение, но и обосновать его, основываясь только на фактах (все задания, сопровождаемые инструкцией «Объясни…», «Обоснуй своё мнение…»).
Работа с математическим содержанием учит уважать и принимать чужое мнение, если оно обосновано (все задания, сопровождаемые инструкцией «Сравни свою работу с работами других ребят»). Таким образом, работа с математическим содержанием позволяет поднимать самооценку учащихся, формировать у них чувство собственного достоинства, понимание ценности своей и чужой личности.
На уроках запланированы ситуации тесного межличностного общения, предполагающие формирование важнейших этических норм. Эти нормы общения выстраиваются в соответствии с правилами и позволяют научить ребёнка грамотно и корректно взаимодействовать с другими. Такая работа развивает у детей представление о толерантности, учит терпению во взаимоотношениях и в то же время умению не терять при общении свою индивидуальность, т.е. также способствует формированию представлений о ценности человеческой личности. (Все задания, относящиеся к работе на этапе первичного закрепления нового, работа с текстовыми задачами в классе и т.д.)
Регулятивные универсальные учебные действия
Регулятивные действия обеспечивают организацию учащимся своей учебной деятельности. Они предполагают умения поставить цель при решении каких-то задач, проблем, составить план действий, получить результат, действуя по плану, и сравнить его с замыслом. Регулятивные действия обеспечивают учащимся:
- умение учиться и способность к организации своей деятельности;
- способность ставить цель и следовать ей в учебной деятельности;
- умение планировать свою деятельности и действовать по плану;
- умение адекватно воспринимать оценки и отметки;
- учебное сотрудничество учителя с учеником на основе признания индивидуальности каждого ребенка.
К ним относятся (Слайд 8):
— целеполагание;
— планирование;
— прогнозирование;
— контроль;
— коррекция;
— оценка;
— саморегуляция.
Целеполагание — постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно; учу учащихся определять и формулировать цель деятельности на уроке; искать средства её осуществления. Стараюсь, чтобы дети самостоятельное выделение познавательной цели на данном этапе обучения.
На какие группы можно разбить эти выражения?
Что общего у выражений в первом столбике, во втором, в третьем?
Какая тема для вас новая?
Сформулируйте тему урока? А наша цель? Чему будем учиться?
Планирование – определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий. Здесь мы проговариваем последовательность действий на уроке; составляем план действий (план урока), план решения задач, выражений и т.д. может быть алгоритм решения выражений.
План может быть выглядеть в печатном виде, же в виде рисунков и схем:
- Устный счет
- Графический диктант
- Работа с геометрическими фигурами
- Нахождение площади фигур сложной конфигурации
- Физкультминутка
- Решение задач
- Тест
- Подведение итогов
- Домашнее задание
2)(Слайд 9.)
3) Прогнозирование – предвосхищение результата и уровня усвоения, его временных характеристик. Ребята учатся высказывать своё предположение (версию) на основе работы с определёнными заданиями; умеют работать в заданном темпе – выбор задания по своим силам.
1) Игра «Моя задача» ( решить одну задачу в решении которой уверен)
Контроль в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
Осуществляется индивидуальная форма работы: учащиеся самостоятельно выполняют задания, осуществляют взаимопроверку или самопроверку; пошагово сравнивая с эталоном, и сами оценивают.
а) Работа по карточкам: найти и посчитать примеры с данными ответами.
7 8 9 Самопроверка
11 – 1 10 – 2 10 + 9 10-3=7 10-2=8 10-1=9
10 – 3 10 + 5 10 – 1 3+4=7 6+2=8 4+5=9
3 + 4 6 + 2 4 + 5 5+2=7 4+4=8 7+2=9
10 + 4 4 + 4 7 + 2 6+1=7 8+0=8 6+3=9
5 + 2 8 + 0 6 – 3
6 + 1 4 – 4 6 + 3
/У каждой пары свои карточки/
б) Индивидуальная работа. Найди нужный ответ.
Взаимопроверка
6 + 2 7 8 9 6+2=8
7 – 4 3 4 5 7-4=3
2 + 3 5 6 7 2+3=7
9 – 3 7 6 5 9-3=6
0 + 5 5 6 7 0+5=5
Коррекция – внесение необходимых дополнений и корректив в план и способ действия в случае расхождения эталона, реального действия и его продукта. Учащиеся предлагают изменение в плане урока, в решениях определённых заданий. Объясняют выбор наиболее подходящего вариантов решения. Это могут быть задача с лишними данными, с недостающими данными, изменение данных, вопроса.
1)Я предлагаю план урока математики: устный счёт, графический диктант, работа с геометрическими фигурами, физкультминутка, нахождение площади фигур сложной конфигурации, решение задач (тест), подведение итогов. Дети вносят свои добавления: вместо решения задач взять тест.
2)Составление задачи по краткой записи и решение .
КУР – 10
на ? меньше
УТОК – 6
Как будем решать задачу?
10 – 6 = 4 (у.)
Ответ: на 4 утки меньше.
Измените задачу так, чтобы она решалась сложением.
Оценка — выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.
В ходе учебной деятельности мы учимся давать оценку своих результатов:
Что нового узнали?
— Что запомнили?
— В чём затруднялись?
Я хочу сказать…
— Я теперь умею…
— Я затруднялся…
Я научился на уроке………………..
На уроке мне понравилось… … …
Урок привлек меня тем………..
Мне показался интересным………..
Заставил задуматься…………
Саморегуляция основана на самооценке школьника, формированием в ходе учебной деятельности рефлексивного отношения к себе, нравственно этическим оцениванием ребёнком своих поступков на основе усвоения системы нравственных норм. На уроке учащиеся дают эмоциональную оценку своей деятельности на данном уроке. Это осуществляется с помощью рефлексии:
1)Выбор своей пословицы :
Терпенье и труд всё перетрут.
Ленивому всегда праздник.
Труд кормит, а лень портит.
Не говори не умею, а говори научусь.
2)«Остров настроения»: карточки с названиями островов: грусть, печаль, радость, непонимание, уверенность.
3)«Лучик солнца»:
Самый длинный лучик – Я уверен в своих знаниях
Средний лучик — Я сомневаюсь в своих знаниях
Самый короткий лучик – Мне очень трудно
4)Барометр настроения : Счастье Скука Уверенность Усталость
и др.
Коммуникативные универсальные учебные действия
Но наряду с всем очевидной ролью математики («ум в порядок приводит») в рамках УМК«Начальная школа XXl века» у этого предмета есть ещё одна важная роль – формирование коммуникативных универсальных учебных действий (Слайд 11).
В процессе изучения математики осуществляется знакомство с математическим языком, формируются речевые умения: дети учатся высказывать суждения с использованием математических терминов и понятий, формулировать вопросы и ответы в ходе выполнения задания, доказательства верности или неверности выполненного действия, обосновывают этапы решения учебной задачи. Работая в соответствии с инструкциями к заданиям учебника, дети учатся работать в парах, выполняя заданные в учебнике проекты в малых группах.
Развиваются базовые умения различных видов речевой деятельности: говорения, слушания, чтения и письма.
Можно отнести все задания, сопровождающиеся инструкциями «Расскажи», «Объясни», «Обоснуй свой ответ», и все задания, обозначенные вопросительным знаком.
К формированию коммуникативных универсальных учебных действий относится система заданий, нацеленных на организацию общения учеников в паре или группе.
Уже начиная с первого класса, стараюсь на уроках использовать парную и групповую работу:
— парная (каждая пара получает задание и выполняет его, прислушиваясь друг к другу, затем отвечают вдвоём или кто-то один по обоюдному согласию).
— групповая (каждая группа получает определенное задание (либо одинаковое, либо дифференцированное) и выполняет его, сообща, под непосредственным руководством лидера группы; задания в группе выполняются таким способом, который позволяет учитывать и оценивать индивидуальный вклад
каждого члена группы. Затем лидер группы или учитель (в исключительных случаях) назначает выступающего).
Кроме того, групповая работа предполагает и проектные задания. На некоторых уроках мы пытаемся составлять мини-проекты нашего урока, например: «Город чисел», « Дом, в котором живёт цифра 5».
Основой развития коммуникативных умений в данном курсе математики является систематическое использование на уроках трёх видов диалога:
а) диалог в большой группе (учитель – ученики);
б) диалог в небольшой группе (ученик – ученики);
в) диалог в паре (ученик – ученик).
Приложения
Список использованных источников
- Асмолов А.Г., Бурменская Г.В., Володарская И.А., Карабанова О.А., Салмина Н.Г. Молчанов С.В. Как проектировать универсальные учебные действия: от действия к мысли. – М., 2010.
- http:// nsportal.ru /nachalnaya-skola/ matematika/ formirovanie-uud
- http://festival.1september.ru/articles/563542/